Research
Here you will find a brief overview of my research interests along with links to relevant publications. A complete list of publications can be found here or on my Google Scholar page.
Adaptive Mesh Refinement - Dendro
My dissertation research on algorithms for constructing and balancing octrees in parallel. Algorithms for fast meshing based on octrees from points and image data were also developed. The mesh is used for solving PDEs on using the finite element method. This work has been extended to include multigrid solvers and is freely available. The work has also been extended to include complex geometries as a forest of octrees (p4est).
Computational Relativity - DendroGR
DendroGR is a portable and highly-scalable infrastructure that is used by the astrophysics and gravitational physics communities. This code combines Dendro with wavelet adaptive multiresolution and physics modules to solve the Einstein equations of general relativity, the relativistic MHD equations, and neutrino leakage. The goal of this work is to perform advanced, massively parallel numerical simulations of IMRIs with mass ratios on the order of 1/100 to generate waveforms that can be used in LIGO data analysis and to calibrate approximate methods. An example of a binary black hole merger is shown below.
Fluids & Immersed Boundary Method - Dendro ==UPDATE==
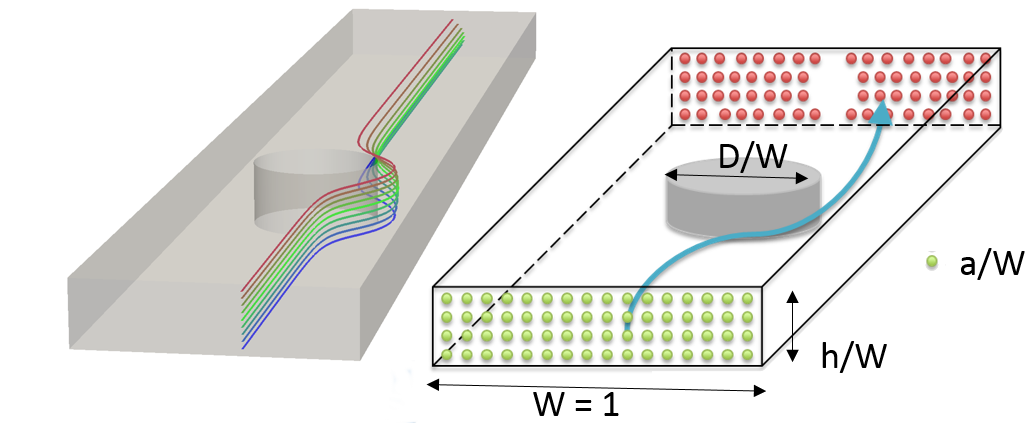
Control and localization of particles (cells, precipitates, etc.) in aqueous flow is useful in biological processing, chemical reaction control, and for creating structured materials. The controlled motion and localization of fluids containing cells and particles can automate processes in cellular sample preparation and bio-sensing. Some examples include fast identification of e. coli in water, robust removal of circulating tumor cells from the blood stream and fast separation of cells types for rapid flow cytometry and subsequent identification/tagging for genomic analysis. The precise, efficient and cheap localization of a heterogeneous collection of cells in a fluid medium is a foundational challenge in science and engineering.
This project, in collaboration with researchers at Iowa State University, is to passively localize particles in fluid flow using a sequence of obstacles that differentially act on various sized particles (based on size and location). Precise calculation needed to design devices that can exploit the migration of particles in flow, such as the separation, concentration, and sorting of cells and biomolecules with high specificity becomes a purely computational exercise. However, tracking particle motion in complex obstructed geometries is a computationally daunting proposition. By coupling the large-scale adaptive meshing of Dendro with Taly, a computational fluid dynamics code, we are able to make these problems computationally tractable. Support for meshes with voids or holes has been added to Dendro for this project.

Domain Specific Languages - Finch
==Add== text on this.
BTE
Multigrid Methods
My postdoc research involved developing parallel geometric multigrid (GMG) methods for solving variable-coefficient elliptic partial differential equations on arbitrary geometries using highly unstructured forests of octrees. We use algebraic multigrid (AMG) as the coarse grid solver for GMG, giving us ability to adjust the number of GMG and AMG levels based on the application. Numerical experiments for the 3D variable-coefficient Poisson problem demonstrate the scalability of our method and our largest run was a highly non-uniform mesh of the earth's mantle, with 80-Billion unknowns using 262,144 cores on NCCS's Jaguar. I am currently working on extending this to support higher-order discretizations. We are currently working on developing Algebraic Multigrid Methods with similar scalability and performance.
Geosciences
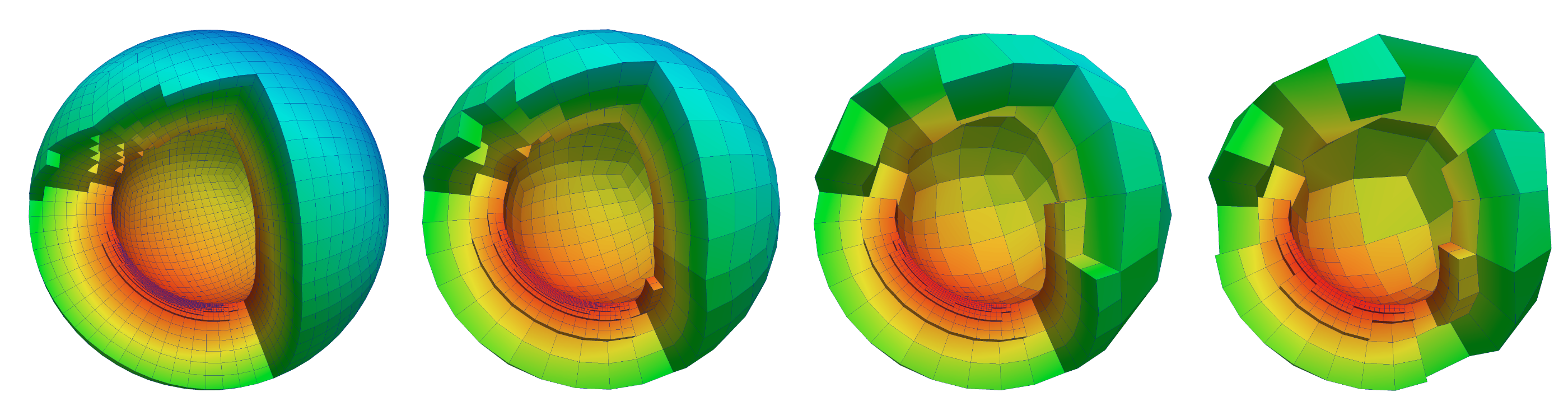
In recent work, we addressed the problem of modeling global-scale, convection-driven flow in Earth’s mantle with associated plate motions. Modeling global mantle flow is a challenging problem due to several inherent difficulties: (1) the severe nonlinearity of the rheology of the mantle, (2) the orders-of-magnitude viscosity contrast and sharp viscosity gradients, and (3) the widely-varying spatial scales. We present scalable numerical methods and their efficient parallel implementation for solving global mantle flow problems that represent a significant improvement over our previous work (e.g., see [1]) in key areas as the discretization as well as the linear and nonlinear solver. In particular, we develop parallel scalable geometric multigrid methods for preconditioning the linearized Stokes systems that arise upon discretization with high-order finite elements on adaptive meshes. We provide numerical results based on real Earth data that are likely the most realistic global scale mantle flow simulations conducted to date, and we demonstrate scalability results on up to 16,384 cores. SC14 Best Poster Award

Data Partitioning (To Be Added)
- FlexPart
- Enclave
Fast Algorithms
- FGT
- HPS
Photonics
Sorting
Although comparison-based sorting is a well studied subject, there are practical issues related to its scalability at large core counts. Specifically scalability of existing approaches deteriorates as the number of processes becomes larger than the average number of records on a process. Sorting is also an enabling algorithm for parallelization as several problems can be addressed by using an efficient parallel sort as a building block. An example of this is the previously mentioned octree construction and 2:1 balance refinement, both of which can be implemented as process-local operations and distributed sorts. In ICS-13, we presented a new in-RAM sorting algorithm, HykSort, where we sustained an in-RAM sort throughput of 54TB/min on 262,144 cores of the CRAY XK7 \emph{Titan} platform at the Oak Ridge National Laboratory. Such a high throughput was achieved by avoiding $\mathcal{O}(p)$-collective communication primitives, ensuring better load balancing and using a staged-communication pattern to avoid network congestion. Given the rate at which data has been growing, the imbalance between what we can fit in memory, and the amount of data we wish to process is only going to increase for the foreseeable future. In SC13, we extended our algorithm to perform out-of-core sorting. By clever use of available storage and a formulation of asynchronous data transfer mechanisms, we are able to almost completely hide the computation (sorting) behind the IO latency. This latency hiding enables us to achieve comparable execution times, including the additional temporary IO required, between a large sort problem (5TB) run as a single, in-RAM sort and our out-of-core approach using 1/10th the amount of RAM. In our largest run, sorting 100TB of records using 1792 hosts, we achieved an end-to-end throughput of 1.24TB/min using our general-purpose sorter, improving on the current Daytona record holder by 65%. We demonstrated sustained throughput on three of the fastest supercomputers in the world --- Titan at the Oak Ridge National Laboratory, Stampede at the Texas Advanced Computing Center and Blue Waters at the University of Illinois at Urbana-Champaign. As the developed out-of-core method tests and stresses nearly all components of modern supercomputing architectures (global IO, local IO, interconnect, local compute performance, etc) we also plan to package the entire process (data delivery plus sort) for use as a standalone, system-level benchmark.
Graph Algorithms
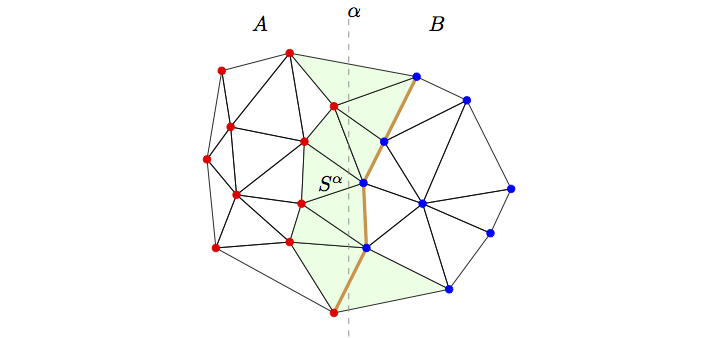
Relative Neighborhood Graphs We present a parallel algorithm for computing cycle orders and cycle perimeters in relative neighborhood graphs (Urquhart approximations) derived from histopathological image data. This algorithm would enable the study of correlations between macroscopic imaging biomarkers of prostate cancer and these important graph-theoretic microscopic biomarkers and may also allow the rapid automated Gleason scoring or cancer detection in prostate biopsy slides. Our algorithm consists of the following steps: (1) Uniform partitioning of the nuclei across processes, (2) Parallel Delaunay triangulation and (3) Parallel computation of the the RNG and the cycle orders and perimeters. We have evaluated our algorithm on a whole-mount histopathology slide obtained after radical prostatectomy. The single-process sequential version of our parallel algorithm offers a significant speed-up over a straightforward sequential algorithm and we demonstrate excellent fixed-size and isogranular parallel scalabity upto 384 processes.
Graph Coloring is a form of graph labeling, wherein we wish to label(color) vertices such that no two adjacent vertices have the same color. It is of interest to my research due to its use in parallelization of algorithms such as the Gauß-Seidel method. I have a simple 2D javascript demo exploring coloring issues on quadtrees.
Biomechanics
My dissertation research involved the development of a method for the analysis of Magnetic Resonance (MR) cardiac images with the goal of reconstructing the motion of the myocardial tissue. The main feature of our method is that the inversion parameter field is the active contraction of the myocardial fibers. This is accomplished with a biophysically-constrained, four-dimensional (space plus time) formulation that aims to complement information that can be gathered from the images by a priori knowledge of cardiac mechanics and electrophysiology. Incorporating biomechanical priors introduces major computational challenges, which constitute the main issue tackled by my dissertation research.
Our main hypothesis is that by incorporating biophysical information, we can generate more informative priors and thus, more accurate predictions of the ventricular wall motion. In this thesis, we outline the formulation, discuss the computational methodology for solving the inverse motion estimation, and present results using synthetic and tagged MR data. We also present methods for generating and solving using a spatially non-uniform octree meshing scheme with an adjoint-based inversion solver. The overall method uses patient-specific MR data and fiber information to reconstruct the motion. Additional information is available on my biomechanics page.