Data Structure: Randomly Choosable Set
The idea was taken from this post by Manish Gupta.
Requirements
We want to devise a data structure that holds a collection of distinct elements and supports the following operations in amortized constant time, \(O(1)\).
add(elem: T): Inserts an elementelemto the collection if not already present.delete(elem: T): Removes an elementelemfrom the collection if present.get_random_element(): Returns a uniformly-random element from the current collection.
Additionally, we consider the following:
- Space efficiency: The data structure should not take too much space with a small collection, and space complexity should be \(O(n)\).
- Determinism: For better reproducibility, we want the
get_random_element()operation to be in a deterministic fashion.
Design
To achieve this, we employ a combination of a dynamic array and inverse table, with which we can search the position of the element in the array. In Python, dict implements the hash table, so the amortized running time of element addition / deletion is \(O(1)\).
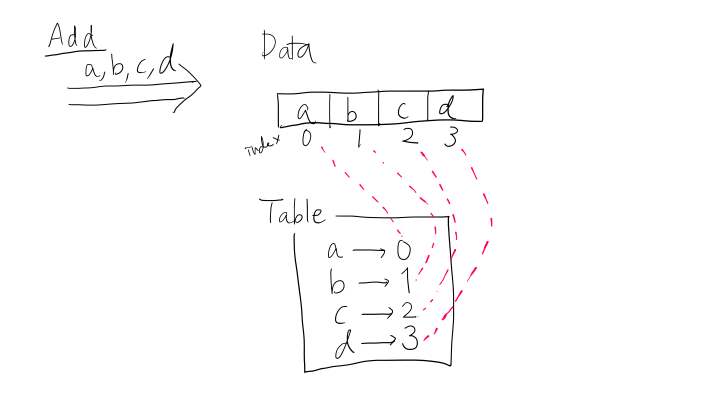
add(elem: T)
When adding an element to the collection, we first check the existence of the element by looking up the inverse table. If it is not present, we insert the element to the last position of the data array and then memorize its index in the inverse table.
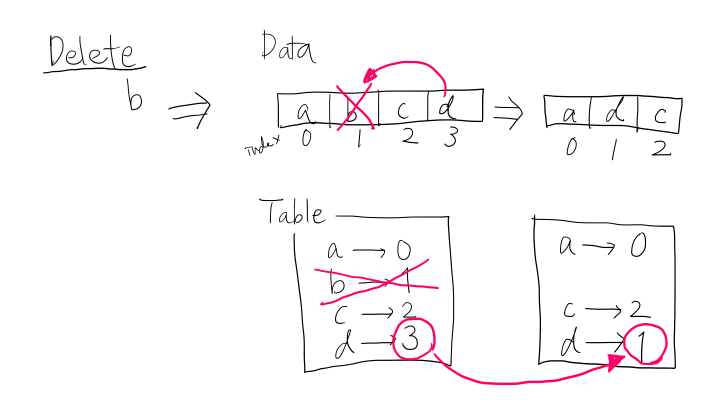
delete(elem: T)
To delete an element, we again look up the inverse table and get the index of the element in the data array. If it is present, we overwrite it by moving the last element in the array to that index. Finally, we maintain the inverse table; delete the entry of the element we want to remove, and update the index of the element that was in the last position of the array.
get_random_element()
We simply pick a random element in the data array. This works in \(O(1)\) because an array is a random access data structure. To ensure determinism, we somehow need to keep track of the state of the pseudo random number generator. We decided to give a seed when constructing the data structure.
Implementation
Here is an excerpt from my implementation.
from typing import Generic, TypeVar
from random import Random
T = TypeVar('T')
class RandomlyChoosableSet(Generic[T]):
"""Set-based data structure that enables efficient uniformly-random
selection.
"""
def __init__(self, seed: int = None) -> None:
"""Creates an instance of RandomlyChoosableSet.
Args:
seed: integer or None (default); Indicator of random number
generation state.
"""
self._init_seed = seed
self._rand = Random(seed)
self._data = []
self._dict = {}
def add(self, elem: T) -> None:
"""Inserts an element to the set.
Runtime complexity: `O(1)`
Args:
elem: Element to add.
"""
if elem in self._dict:
# element already exists
return
self._dict[elem] = len(self._data)
self._data.append(elem)
def delete(self, elem: T) -> None:
"""Removes an element from the set.
Runtime complexity: `O(1)`
Args:
elem: Element to delete.
Raises:
KeyError: If `elem` is not in the set.
"""
if elem not in self._dict:
# element does not exist
raise KeyError(elem)
index = self._dict[elem]
del self._dict[elem]
# swap with the last element
if (len(self._data) > 1 and index != len(self._data) - 1):
self._data[index] = self._data[-1]
self._dict[self._data[index]] = index
# remove data
self._data.pop()
def get_random_element(self) -> T:
"""Randomly chooses an element in the set. The random state may or
may not change.
Runtime complexity: `O(1)`
Returns:
Random element in the set or None if the set is empty.
"""
if len(self._data) == 0:
return None
elif len(self._data) == 1:
return self._data[0]
index = self._rand.randint(0, len(self._data) - 1)
return self._data[index]
I would also suggest implementing other utility functions, such as __contains__, __len__, and __eq__. Those should be pretty straightforward.
def __contains__(self, elem: T) -> bool:
"""Returns if the element is in the set.
Runtime complexity: `O(1)`
Args:
elem: Element to check.
Returns:
True if `elem` is in the set.
"""
return elem in self._dict
Notes on determinism
Astute readers may have noticed that the randomness of the method get_random_element() relies on the internal data structure, self._data. That being said, the history of addition and deletion may affect the selection process.
For instance, if we add a, b, c in this order, the self._data will be ['a', 'b', 'c']. On the other hand, if we add b, c, a in this order, it will result in ['b', 'c', 'a']. Even if the pseudo random number generator chooses the same number, the result will vary. A similar situation occurs when, for example, we add x, a, b, c and then delete x because x will be swapped with the last element c.
How can we solve this issue? In other words, can we choose an element deterministically regardless of the operation history? One option is to use other data structures like balanced search trees. It seems like the library Sorted Containers does the excellent work, but the running time of each operation will now become \(O(\log n)\) instead of \(O(1)\).